Ch6主要是对机器学习中的分类问题进行建模。

“逻辑斯提克回归”的名字来源是源于Logistic函数，因为有用到线性回归的函数，所以合称为“Logistic Regression”。首先对二分类问题进行讨论，定义了新的损失函数，并对该损失函数的来源（极大似然估计）以及损失函数的梯度下降法进行了推导。

多分类问题是在二分类问题上的进一步延伸。

Ch4主要是对机器学习中的多元回归问题进行建模，这里的多元指的是多个特征。其中特征可以由多个单特征构成，也可由单特征的指数/对数/次方…等运算项构成。
假设函数取线性公式；损失函数仍然采用了均方差公式。除了用梯度下降法进行参数更新外，还提出了正规方程法，可以一步到位计算出参数，但也有其局限所在。

针对数值特征，进一步提出能加快梯度下降法迭代速度的归一化概念。

EfficientDet

现行构建目标检测模型的思路

随着迁移学习概念的兴起和普及，目标检测和图像分类这两个任务具有一定的相似性，因为可以将分类的网络，比如VGG、ResNet等，用来做特征提取器。这一部分，我们就称其为backbone。

所谓的backbone，直接翻译过来就是“骨干网络”，非整体网络。因为分类与检测非等价。OD(Object Detection)需要对物体进行定位和分类，仅仅是微调网络是无法完成OD任务的，在后面加一些网络层，让这些额外加进来的网络层去弥补分类网络无法定位的先天缺陷。

具体做法就是在检测任务的数据集对分类网络进行微调。

脉络就非常清晰了：分类网络迁移过来，用作特征提取器（通过在OD数据集上进行微调，并且与后续的网络的共同训练，使得它提取出来的特征更适合OD任务），后续的网络负责从这些特征中，检测目标的位置和类别。那么，我们就将分类网络所在的环节称之为“Backbone”，后续连接的网络层称之为“Detection head”。

为了更地检测各种大小的物体，一些多尺度技术提了出来，最经典的，莫过于《Feature Pyramid Networks for Object Detection》提出的FPN结构，在不同的尺度（实际上就是不同大小的feature map）上去提取不同尺度的信息，并进行融合，充分利用好backbone提取的所有的特征信息，从而让网络能够更好地检测物体。

建模背景

目标检测模型越来越大，计算量也越来越大，而一些模型提高了效率但同时也降低了精度。EfficientDet的目的就是为了同时满足高精度和高效率，达到了低参数量，模型小。

高效目标检测算法设计的两个主要挑战就是：(1)多尺度特征融合；(2)模型缩放。

前者是为了更有效的检测，后者是为了让模型更小更便于落地应用。

EfficientDet的结构

特征提取使用EfficientNet，以此为backbone。

图像的特征有很多，作用也不相同，因此应该对不同的特征赋权。使用BiFPN作为为多尺度特征融合的解决方案。对分类层的分类特征进行加权融合，作为类别预测网络和锚框定位网络的输入。

具体的框架如下图：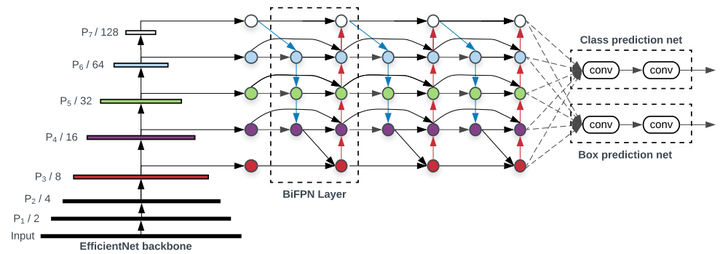

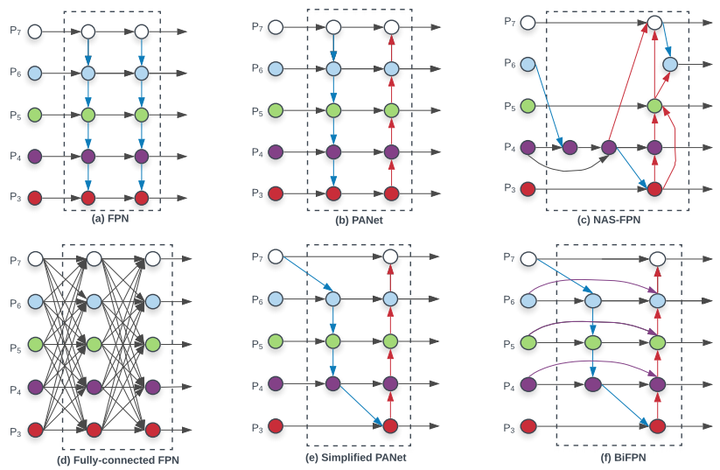
多尺度特征融合

传统的top-down FPN只有自顶向下单向信息流，PANet增加了自底向上的信息流，NAS-FPN通过大量计算和搜索有更复杂的信息流。本文对不同FPN实验发现，PANet的效果最佳，但参数量计算量也较大（见后文Ablation实验）。本文在PANet的基础上提出三步优化[2]：1)去掉没有进行融合的单一特征图参数学习（这里感觉本文对PANet是不是有些误解，个人理解PANet提出的就是简化的版本）；2)同一层中增加从原始节点到输出节点的短接；3)堆叠FPN结构。 =>BiFPN

模型缩放

模型缩放，即模型复杂度调整。

【需补充】 EfficientNet 时间不足，未去深度了解，只知道是需要在三个维度进行同一缩放，效果较好，提出了一个同一缩放的复合参数$\Phi$。

在EfficientDet基础上，提出了OD模型复杂度联合调整方法，联合调整了backbone、FPN、prediction网络的depth、width、resolution。

scaling 是什么意思？
对CNN模型做三种缩放维度：depth, width, and resolution. 直观的说，depth scaling是调整网络的深度，width scaling是调整卷积层中feature map的数量，resolution scaling是调整输入图像分辨率的大小。

与EfficientNet不同，由于参数多采用网格搜索计算量大，EfficientDet采用启发式的调整策略。通过不同的backbone选取，对模型参数量进行比对。

训练细节

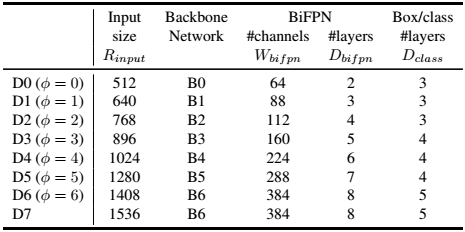
采用SGD，momentum=0.9，weight decay=4e-5，学习率采用5%步数来warmup从0到0.08，然后cosine decay(cosine式衰减学习率)。每层卷积后加batch normalization，batch norm decay 0.997 and epsilon 1e-4。batch size=128在32个TPU。采用focal loss，参数α=0.25，γ=1.5。anchor ratio是{1/2，1，2}。

参考
weight decay（权值衰减）：可以防止过拟合，在损失函数中，weight decay是放在正则项（regularization）前面的一个系数，正则项一般指示模型的复杂度，所以weight decay的作用是调节模型复杂度对损失函数的影响，若weight decay很大，则复杂的模型损失函数的值也就大。
momentum是梯度下降法中一种常用的加速技术，加速参数收敛的过程。
batch normalization批标准化是指在神经网络中激活函数的前面，将按照特征进行normalization。因为深层神经网络在做非线性变换前的激活输入值（就是那个x=WU+B，U是输入）随着网络深度加深或者在训练过程中，其分布逐渐发生偏移或者变动，之所以训练收敛慢，一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近（对于Sigmoid函数来说，意味着激活输入值WU+B是大的负值或正值），所以这导致反向传播时低层神经网络的梯度消失，这是训练深层神经网络收敛越来越慢的本质原因，而BN就是通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0、方差为1的标准正态分布，其实就是把越来越偏的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，意思是这样让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。所以BN的好处有三点：

1. 提高梯度在网络中的流动。Normalization能够使特征全部缩放到[0,1]，这样在反向传播时候的梯度都是在1左右，避免了梯度消失现象。
2. 提升学习速率。归一化后的数据能够快速的达到收敛。
3. 减少模型训练对初始化的依赖。

​
深入理解Batch Normalization批标准化
什么是批标准化 (Batch Normalization)

【未弄懂，需细看】参考
learning rate warm up：训练初期由于离目标较远，一般需要选择大的学习率，但是使用过大的学习率容易导致不稳定性。所以可以做一个学习率热身阶段，在开始的时候先使用一个较小的学习率，然后当训练过程稳定的时候再把学习率调回去。比如说在热身阶段，将学习率从0调到初始学习率。举个例子，如果我们准备用m个batches来热身，准备的初始学习率是n,然后在每个$batch_i,i<=i<=m$,将每次的学习率设为$in/m$。

• 有助于减缓模型在初始阶段对mini-batch的提前过拟合现象，保持分布的平稳
• 有助于保持模型深层的稳定性

cosine learning decay CNN训练分类任务的优化策略

Focal Loss 就是一个解决分类问题中类别不平衡、分类难度差异的一个 loss
讨论链接
如何更好地理解「Focal Loss」

实验

用不同的EfficientNet为backbone生成的EfficientDet与其他网络进行对比。小网络EfficientDet-D0和YOLOv3差不多精度，计算量少28倍；EfficientDet-D1和RetinaNet、MaskRCNN差不多精度，参数量少8倍，计算量少25倍。总的来说，EfficientDet精度速度双丰收，最高精度达到51.0 mAP，登顶COCO检测榜单。

Ablation experiment

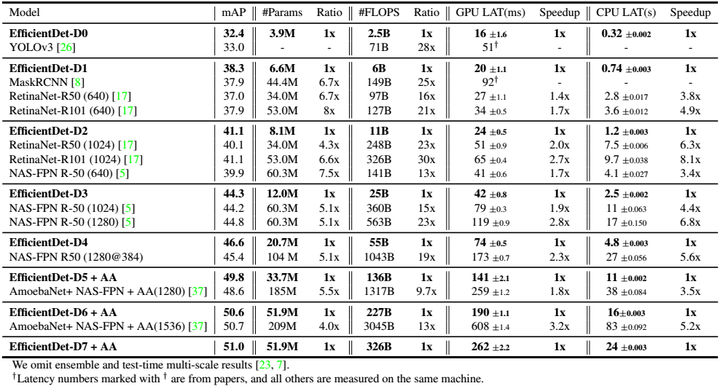
Ablation experiment， 消融实验就是用来告诉读者整个模型里面的关键部分到底起了多大作用，用更直观的数据来说明算法的有效性。

分别替换EfficientNet和BiFPN，结果看出两者都显著提升mAP。（BiFPN结构比FPN要更复杂，参数量少应该是因为采用了depthwise conv）

将各种FPN分别进行五次实验，对比看出设计的BiFPN和PANet效果相当，使用更少的参数量和计算量，使用学习的加权和会有一点提升。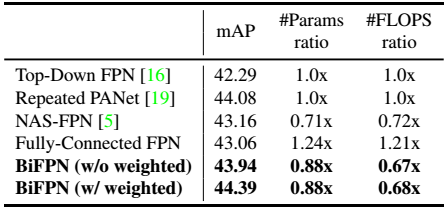

w/o=without,w/=with

权重归一化时采用线性比Softmax速度更快，达到同等精度。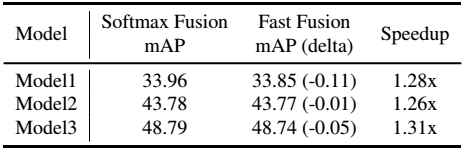

联合调整策略明显优于所有单独调整的策略。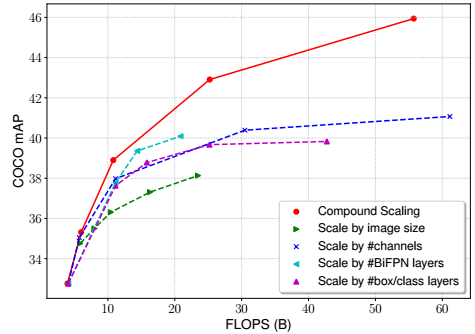

亮点总结

最大的亮点在于提出了目标检测网络联合调整复杂度的策略，从而在COCO上达到51.0 mAP的最优成绩。一部分原因是EfficientNet，而EfficientNet的Baseline是通过NAS得到的。

第二亮点，堆叠FPN，通过堆叠FPN，BiFPN的设计有效，增加短接以及学习加权和，能达到很好效果。

Benchmark vs. Baseline 参考
benchmark一般是和同行中比较牛的算法比较。benchmark的性能已经被广泛研究，人们对它性能的表现形式、测量方法都非常熟悉，因此可以作为标准方法来衡量其他方法的好坏。state-of-the-art（SOTA）的算法表明其性能在当前属于最佳性能。

baseline一般是自己算法优化和调参过程中自己和自己比较，目标是越来越好。baseline有一个自带的含义就是“性能起点”，指的是对照组，基准线，就是你这个实验有提升，那么你的提升是对比于什么的提升，被对比的就是baseline。

NAS (Neural Architecture Search) 神经架构搜索
自己设计，代价昂贵，也有可能非当前最先进。NAS是一种自动设计神经网络的技术，可以通过算法根据样本集自动设计出高性能的网络结构，可以有效的降低神经网络的使用和实现成本。

NAS的原理是给定一个称为搜索空间的候选神经网络结构集合，用某种策略从中搜索出最优网络结构。神经网络结构的优劣即性能用某些指标如精度、速度来度量，称为性能评估。

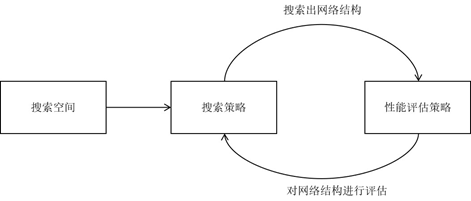
搜索空间，搜索策略，性能评估策略是NAS算法的核心要素。搜索空间定义了可以搜索的神经网络结构的集合，即解的空间。搜索策略定义了如何在搜索空间中寻找最优网络结构。性能评估策略定义了如何评估搜索出的网络结构的性能。

在搜索过程的每次迭代中，从搜索空间产生“样本”即得到一个神经网络结构，称为“子网络”。在训练样本集上训练子网络，然后在验证集上评估其性能。逐步优化网络结构，直至找到最优的子网络。

mAP的具体解释可见本站【目标检测评价指标.md】这篇文章。

更近一步

[1]目标检测实战资料贴https://zhuanlan.zhihu.com/c_1178388040400302080

HOG全称histogram of oriented gradients。如果翻译成中文就是方向梯度直方图。它可以用来表示图像的物体特征，因此能够检测出这类物体。参考

目标检测的评价指标：

• 精度评价 mAP（mean Average Precision）：即各类别AP的平均值
• 速度指标
  • (1)检测器每秒能处理图片的张数 FPS：在同一硬件条件下，每秒处理的图片数量或者处理每张图片所需的时间
  • (2)检测器处理每张图片的时间
  • 相当于$x=v \times t$

语言模型

自然语言处理的重要技术。自然语言文本是一段离散的时间序列，长度为T的文本各词w_t的出现可认为在时间步t的输出。语言模型会计算词序列的概率，判断哪种组合出现概率最大，作为最终输出。

优化与深度学习

损失函数最小化=目标函数最小化

优化目标=训练误差降低

DL 目标=泛化误差降低；除了应达到优化目标外，壬戌要应对过拟合问题。

目标函数过于复杂，故优化问题找数值解。挑战有：

1. 局部最小值
2. 鞍点

局部最小值

局部最小值点梯度为0，故很容易陷入其中，全局最小化难以满足。

鞍点

梯度为0的三种可能：

• 全局最小值
• 局部最小值
• 鞍点

np.mgrid[]用法

Hessian矩阵：梯度向量的梯度向量，输出关于输入的偏导数矩阵。

• Hessian矩阵在梯度为0的位置特征值全正，函数取局部最小值。
• Hessian矩阵在梯度为0的位置特征值全负，函数取局部最大值。
• Hessian矩阵在梯度为0的位置上特征值有正有负，函数有鞍点存在。

随机矩阵理论：高斯随机矩阵，任一特征值的正负概率均为0.5，故第1、2种概率均只有0.5^k，鞍点比局部极小值更为常见。

深度学习中找全局最优解并非必要。

梯度下降和随机梯度下降

一维梯度下降

逆梯度目标函数值下降最快。
学习率：

• 过小，迭代时间长
• 过大，泰勒展开公式不成立，发散
• 合适的lr需要通过多次实验得到

多维梯度下降

逆梯度方向可使方向导数最小化，降低目标函数值。

随机梯度下降

深度学习中的目标函数常常是训练集中各个样本损失函数的平均。

梯度下降的每次迭代时间复杂度为Ｏ(n)，随机梯度下降法可以减少每次迭代的计算开销，从n个样本中选一个计算梯度，应用梯度下降更新参数。

随机梯度是对梯度的无偏估计。

小批量随机梯度下降

梯度下降法用整个训练集来计算梯度，batch gradient descent;随机梯度下降法选择一个样本来计算梯度，而小批量随机梯度下降则用一个样本组来计算梯度（平均）。

重复采样：允许同一个小批量中出现重复的样本。
不重复采样：不允许同一小批量中出现重复样本，更常见。

重复采样所得的小批量随机梯度是对梯度的无偏估计。

基于随机采样得到梯度的方差在迭代过程无法减小，实际过程中要将学习率进行衰减(在小批量和随机中都要)；而梯度下降在迭代过程中使用的目标函数的真实梯度，无需衰减学习率。

随着迭代计算开销的增大，随机梯度下降-》小批量随机梯度下降-》梯度下降。批量的选择很重要，少了并行处理和内存使用效率低，大了梯度中冗余信息较多。批量较大时，增大迭代周期数。

动量法

梯度下降法的问题

针对不同的参数的梯度量级，难以找到统一的学习率进行迭代更新，往往造成发散。

动量法思路

对最近的1/(1-r)个时间步的更新量（学习率x梯度）进行指数加权平均后再除以1-r，权重按时间步指数衰减。自变量在各个方向的移动幅度不仅与当前梯度有关，而且与过去梯度在各方向是否一致有关。使得相邻时间步的自变量更新在方向上更加一致。

AdaGrad算法

用同一个学习率来迭代各自变量，但在自变量梯度有较大差异时需要选择足够小的学习率使得自变量在梯度值较大的维度上不发散，但同时也会在梯度值较小维度迭代过慢。

动量法用指数加权移动，使得自变量更新方向更加一致，降低发散可能性。

AdaGrad算法更具自变量在每个味的的梯度值大小调整各个维度学习率，避免统一lr的困惑。

自变量拥有自己的学习率，梯度大的lr下降块，而梯度小的lr变化不大。

公共学习率上s_t一直在累积，最终有可能无法得到有效解。

RMSProp算法

以AdaGrad算法为模版，结合动量法加权随时间步衰减思想，按元素平方做加权，t-1步前加权r，当前加权1-r。解决了各自变量学习率一直降低/不变的问题。

​

AdaDelta算法

改进了AdaGrad算法在迭代后期难以找到有用解的难处，且没有学习率。

用了RMSProp的模板，用自变量更新量平方的指数加权和来替代学习率。

Adam算法

在RMSProp算法基础上对小批量随机梯度做了指数加权和，可看作RMSProp与动量法的结合。

对迭代的中间变量做了偏差修正，目标函数自变量都拥有各自的学习率。

NiN

串联多个NiN块构成小网络来构成深层网络。

命令式和符号式编程

命令式：编程方便，直观理解，调试容易，运行慢，受限多。

符号式：不依赖特定运行环境，高效运行。

混合式：取两者之长。

异步计算

默认情况，Pytorch的GPU操作是异步的。当调用一个使用GPU函数，会排队而非立即运算，允许我们并行更多运算，包括在CPU和GPU。
？？？

自动并行运算

synchronize v.使同步

Pytorch支持多GPU的并行运算。

多GPU计算

单主机多GPU计算，非分布式计算。
如何看显存、利用率？？？

Pytorch可以调用多个特定的GPU进行模型训练。
保存多GPU训练的模型注意仅保存核心层。

图像增广

对训练图像做一系列随即改变，产生相似却不同的训练样本，增大训练数据集的规模。也可降低模型对某些属性的依赖，从而提高模型的泛化能力。

show_images函数进行图片缩放，figsize相应改变，而新图片的每个像素都相应的改变。

图像数据集读取后规格为[image,label]。

Ch2主要是对机器学习中的回归问题进行建模，以及对损失函数相关问题进行了数学上的推导分析。本篇笔记除了对以上进行归纳外，也用Matlab实现了线性回归问题的解决。